http://nippon.zaidan.info/seikabutsu/2003/00136/mokuji.htm

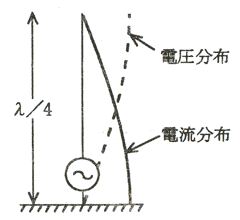
第3章 電波工学の基礎 　 3・1 電波とはなにか 3・1・1 電波の発生 　アンテナに電流を流すと1・2・2項で説明したように磁力線が発生する。電子と陽子が移動すると電流になることを1・3・2項で説明した。アンテナに電流を流すと図3・1に示すようにアンテナを取り巻く磁力線が発生する。アンテナに電流を流すことはマイナスの電子とプラスの陽子が移動することによるのでアンテナ上の陽子の位置から電子の位置に向かい電気力線が発生して図3・1に示すようにアンテナと同じ方向に電気力線が現れる。アンテナに高周波電流を流すと電気力線と磁力線が電波となって放射される。 　 図3・1 アンテナ電流による磁力線と電気力線の発生 　 　送信機から高周波電流を流すとアンテナ電流が周期的に磁力線と電気力線をアンテナから空中に押し出して電波として放射する。電波は電気力線と磁力線が空中を伝搬するので電気磁気波であるが省略して電磁波となり， さらに短く電波と呼ぶようになった。 　アンテナを電波法で空中線と呼ぶ。図3・2に空中線から電気波（電気力線）と磁気波（磁力線）が放射されて伝搬する状態を描いてある。垂直に空中線を置くと電気波は垂直面内を波状に伝搬する。これは電気力線が垂直面内に生じるからである。磁力線は水平面内に生じるので磁気波は水平面内で波状となり伝搬する。電気波と磁気波はお互いに直交した面内に沿って進行する。電波の進行方向に対して電気波と磁気波の振動は横方向となっているので電気的横波とも呼ばれる。図3・2のように電気波が垂直面内にある電波を垂直偏波という。アンテナを横に置くと水平偏波となる。 　 図3・2 アンテナからの電波の伝搬 　 　垂直偏波で送信された電波は垂直に置いた受信アンテナで受信する。中波ラジオは垂直偏波で， テレビとFM放送の電波は水平偏波で送信−受信されている。 　 3・1・2 電波の波長と周波数 　図3・3に電波の周波数と波長との関係を示す。 　 図3・3 電波の波長と周波数の関係 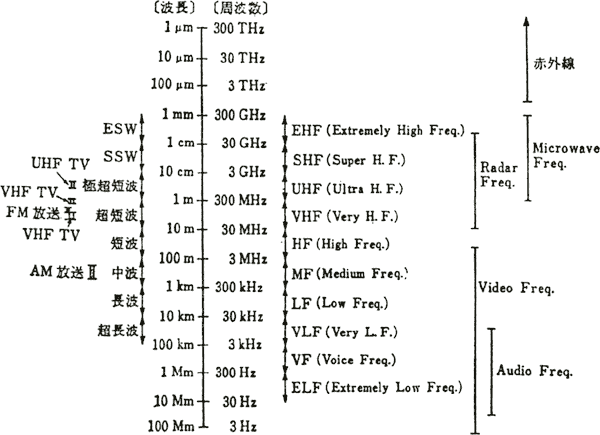　 　周波数3kHz（波長1000km）の長波から300GHzまでが電波法の対象となるが国際電気通信連合， ITUにより光や赤外線等の電気振動はすべて電磁波の定義に含まれるようになった。 　電波の波長と周波数との関係は 電波の速度C＝周波数f×波長λ　（3・1） で計算される。ここで 大気中での伝搬速度c≒3×108　（m/s） 周波数f　（ヘルツ， Hz） 波長λ　（メートル， m）；λはギリシャ語でラムダと読む。 　（3・1）式に空中の電波の伝搬速度を代入すると波長は 波長λ＝電波の速度c／周波数f ≒3×108／周波数f　（m）　（3・2） 又は 周波数≒3×108／波長λ　（Hz）　（3・3） として計算できる。 　 例題1. 周波数100（MHz）の電波の波長はいくらか？ 解答1. メガヘルツ（MHz）をヘルツ（Hz）に換算して 100MHz=100×106=1×108（Hz） （3・2）式より 波長λ＝3×108／1×108＝3（m）， と求められる。 例題2. 波長2mの電波の周波数はいくらか？ 解答2. （3・3）式より 周波数f=3×108／2=1.5×108＝150×106(Hz)=150(MHz) 　 3・2 電波伝搬と電離層 　アンテナから放射された電波は地上波と空間波となって伝搬する。図3・4に電波の伝搬状況を示す。 　 図3・4 電波の伝搬 　 　 に分類される。 　図3・5に電離層と電離層波の伝搬を示す。 　 図3・5 電離層波の伝搬 　 　電離層は太陽から放射される微粒子や紫外線により大気中の酸素や窒素等のガスが電離されてプラスとマイナスに帯電したイオンの雲が地球の上空に形成されたもので， 電波を反射したり， 進路を曲げたりして空間波をつくる。高度約50kmのD層は太陽からの紫外線によるもので波長が長い長波を反射する。E， F層は太陽からの放射微粒子によりつくられる。E層は高度約100kmで中波の進路を曲げて地上に降ろす役目をする。F層の高度は約200kmあり， 昼間はF1とF2に分かれるが夜間に合体して1つの層となる。F層は短波の進路を曲げて地上に降ろす。周波数が高くなるほど高い電離層で反射される。超短波やマイクロ波はすべての電離層を突き抜けるので地上波しか利用できない。 　人工衛星は電離層より高い軌道を持つので電離層を突き抜ける超短波やマイクロ波が使用される。より高い周波数のミリ波を宇宙通信に利用すると大気中の雨による減衰が大きくなる。夜間に遠くの中波放送が聞こえるのはD層内の減衰が少なくなり， D層を突き抜けてE層で反射された中波の空間波が地上に届くから遠くの放送が聞こえるようになる。

3・3・2 アンテナとアース（接地） 　アンテナにはアースをとる接地型とアースが不要な非接地型アンテナがある。図3・8（a）， （b）のダイポールアンテナは非接地型で， （c）の垂直アンテナは接地型アンテナである。 　 図3・8 非接地型アンテナと接地型アンテナ 　 　非接地アンテナは大地の影響を受けないようにできるだけ高く設置する。接地アンテナは（c）の点線で示した地中の映像アンテナを形成させるためにアース線で大地と結合させる必要がある。海上で使用する場合はアース線を海中に投入する。 　 3・3・3 アンテナの共振 　アンテナに高周波電流を供給するとアンテナ線上に電流と電圧が分布する。アンテナの長さが1/2波長の整数倍のときアンテナが共振して能率よく電波が発射される。 　図3・9にアンテナ長が（a）1/2波長， （b）1波長及び（c）2波長のときの電圧と電流の分布を示す。（a）をダイポールアンテナと呼び， 基準アンテナとなっている。（a， c）は中央の給電部で電流が最大で電圧が最小となり， アンテナの端では逆に電流が最小， 電圧が最大となる。アンテナの長さにより異なる電波の指向性を生じる。 　 図3・9 アンテナの電流分布と電圧分布 　 　図3・10に1/4波長接地型アンテナの電流と電圧の分布を示す。接地（アース）をとることにより地中に1/4波長の影像アンテナが形成されアンテナ長が2倍の1/2波長ダイポールアンテナとして動作する。影像とは鏡に姿を映すときに鏡の中に自分の姿が見えるのと同じ原理である。地中に1/4波長の影像アンテナが電気的に形成されるので地上の1/4波長アンテナと合わせた1/2波長垂直ダイポールアンテナを形成する。 　1/4波長接地型垂直アンテナは1/2波長垂直ダイポールアンテナと同じ垂直面内の指向性を持つ。 　 図3・10 1/4波長アンテナ 　 図3・11 ダイポールアンテナと等価回路 　 　図3・11に水平ダイポールアンテナと電気的等価回路を示す。アンテナ導体はインダクタンスLe， 大地との間に容量Ce及びアンテナ抵抗Reを持つ。アンテナ抵抗は 　 Re=RΩ+RA　（3・6） 　 となる。RΩはアンテナ線の導体抵抗で， オームの法則による電力損失分である。RAが電波として放射されるアンテナ電力の抵抗で， アンテナ実効抵抗と呼ばれる。RΩが小さくてRAが大きいほど能率よく電波が放射できる。 　アンテナの共振周波数fr（Hz）と等価回路定数との関係は 　 　 アンテナ放射電力PA（W）は 　 PA=(IA)2×RA　（3・8） 　 で計算される。IAは給電部におけるアンテナ電流である。 　図3・12に開口面アンテナの例を示す。（a）角錐ホーン， （b）円錐ホーンのように開口部から直接電波が前方に放射されるか， （c）反射板付きダイポールのように反射板により反射した電波を放射するアンテナがある。開口面を大きくするほど電波が集中して鋭い指向性のビームとなって前方に放射できる。 　パラボラアンテナの指向性を図3・13に示す。放射電力が最大値の半分となる放射ビームの幅をアンテナの半値指向幅θ-3dBとする。電力が半分の値はデシベル表示で最大値より-3dB電力が低くなる指向幅である。電界では-6dB（0.707）となる。 　 図3・12 開口面アンテナの例 　 図3・13 パラボラアンテナの指向性 　 　半値幅の指向性は 　 　 　ここで， ηは開口面能率でアンテナ面上の電流分布などにより0.6〜0.8の値となる。D＝パラボラの直径， λ＝波長， π＝円周率を（3・9）式に代入すると， パラボラアンテナの指向性は 　 　 として計算される。 　 3・3・4 アンテナ利得 　（3・10）式に示すようにアンテナを大きくするほど指向性が鋭くなり， 目的方向へ大きな電力を放射することができる。アンテナからある距離離れた地点で放射電力を受信する場合を考える。指向性を持つあるアンテナで受信した電力をPθとする。同じ電力を指向性がない等方性アンテナで放射したときの受信電力をP0としたときそのアンテナの利得Gθは 　 　 で定義する。等方性アンテナを基準にした利得を絶対利得と呼ぶ。 　ダイポールアンテナを基準にしたアンテナ利得を相対利得GDで表示する。 　相対利得から絶対利得を求めるには 　 絶対利得G0（dB）＝相対利得GD（dB）＋ダイポール利得2.15（dB）　（3・12） 　 で換算できる。ダイポールアンテナの絶対利得は2.15（dB）である。 　パラボラアンテナの絶対利得は 　 　 　ここで， ηはアンテナの開口能率定数で0.6〜0.8の値， Aはパラボラの面積で， アンテナの直径Dより（3・14）式で計算できる。

3・3・5 アンテナの延長と短縮 　図3・14に携帯型無線機に使用されるむち（ホイップ）アンテナとその指向性を示す。水平面内で等方性（無指向性）となる1/4波長接地型アンテナである。中波や短波帯ではアンテナの長さを1/4波長にするとアンテナが長くなるので短くしたい場合がある。アンテナはインダクタンスLe， 電気容量Ce及び抵抗Reの直列共振回路と等価となることを図3・10により説明した。 　 図3・14 むち（ホイップ）アンテナと指向性 　 　アンテナ回路にコイルやコンデンサーを挿入することにより共振周波数を変化させることができる。 　 図3・15アンテナの電気的延長と短縮 　 　図3・15（a）のように延長コイルLlを挿入すると合成インダクタンス（Le+Ll）が大きくなるので共振周波数が低くなり， アンテナを電気的に延長したことになる。（b）のように短縮コンデンサCsを挿入すると合成容量Ce・Cs/(Ce+Cs)が小さくなるので共振周波数が高くなり， 電気的にアンテナ長を短縮したことになる。 　アンテナが短くて共振がとれない場合は延長コイル， 逆にアンテナが長過ぎる場合は短縮コンデンサをアンテナの一部に挿入することにより電気的にアンテナ長を変化できるので能率よく電波を発射することができるようになる。 　中波放送用垂直アンテナの頂上に容量環と呼ぶ環状のアンテナを乗せるとアンテナ上部の電流が増加して水平方向の放射電力が増加することからサービス区域を増加できる。アンテナの電流分布を変化させると共振周波数や指向性を電気的に変化できるのでアンテナの能率が向上する。 　 第3章 練習問題

第5章 電気・電子・高周波計測の基礎 　 5.1 単位系 　長さの単位はメートル，m，質量の単位はキログラム，kg，のように電圧の単位にボルト，V，電流の単位に，アンペア，A，として電気の量にも単位が用いられる。単位系には大きさの単位と性質（次元）が国際的に規定される。単位系の始めは電気量間に作用するクーロンの電気力の法則から規定されるcgs静電単位系（c.g.s.e.s.u.）と磁気量間に作用するクーロンの磁気力の法則から規定されたcgs電磁単位系（c.g.s.e.m.u.）とから表5・1に示すように順次変化されて現在の国際単位系（SI単位系）になった。 　 表5・1 電気単位系の変遷 　 　国際単位系またはSI単位系は電磁単位系を基礎とした世界共通な単位系でわが国では1967年7月1日から施行された。表5・2に国際単位系を示す。（a）は基本単位で長さ，質量等5つの量で構成される。（b）は電気に関係した量を含む組立単位である。それぞれの量の単位名と記号（次元）も示した。表5・3は量の大きさを変換するための接頭語である。103はキロ，kのように大きさの名称が変わる。 　 表5・2 国際単位の量，単位の名称と記号 （a）基本単位 量 単位 記号 長さ 質量 時間 電流 熱力学的温度 物質量 光度 メートル キログラム 秒 アンペア ケルビン モル カンデラ m kg s A K mol cd 　 （b）組立単位 量 単位 記号 面積 平方メートル m2 体積 立方メートル m3 周波数 ヘルツ Hz 密度 キログラム毎立方メートル kg/m3 速さ メートル毎秒 m/s 角速度 ラジアン毎秒 rad/s 加速度 メートル毎秒毎秒 m/s2 角加速度 ラジアン毎秒毎秒 rad/s2 力 ニュートン N， kg・m/s2 圧力 ニュートン毎平方メートル N/m2 粘度 ニュートン秒毎平方メートル Ns/m2 動粘度 平方メートル毎秒 m2/s 仕事、エネルギー、熱量 ジュール J， N・m 仕事量 ワット W， J/s 電気量 クーロン C， A・s 電圧 ボルト V， W/A 電界の強さ ボルト毎メートル V/m 電気抵抗 オーム Ω， V/A 静電容量 ファラド F， A・s/V インダクタンス ヘンリー H， V・s/A 磁束 ウエーバー Wb， V・s 磁束密度 テスラ T， Wb/m2 磁界の強さ アンペア毎メートル A/m 起磁力 アンペア A 光束 ルーメン lm 輝度 カンデラ毎平方メートル cd/m2 照度 ルクス lX， lm/m2 放射能 毎秒 g-1 　 表5・3 接頭語 倍数 名称 記号 倍数 名称 記号 1018 エクサ E 10-1 デシ d 1015 ペタ P 10-2 センチ c 1012 テラ T 10-3 ミリ m 109 ギガ G 10-6 マイクロ μ 106 メガ M 10-9 ナノ n 103 キロ k 10-12 ピコ p 102 ヘクト h 10-15 フェムト f 10 デカ da 10-13 アト a 　 5・2 デシベル（dB） 　ある数AがBの何倍あるかはAをBで割算すると求められる。割算は分数でも表されるので 　 　 となる。図5・1にある増幅回路を示す。入力電圧，Viと出力電圧VOの比を増幅度GVと呼び 　 　 となる。 　 図5・1 増幅器と増幅度 　 　音を増幅するときの出力を人間が耳で聞くと増幅度GVが10，100，1000，と大きくなっても耳の感覚では出力が20，40，60，・・・倍にしか感じない。人間の感覚器官が刺激の変化に対して対数的に感ずることをウェバーとフェヒナーの二人の生物学者が発見している。音響機器やテレビのように人間の感覚に対する電子機器が多い。 　図5・1の（　）内に示すように生物として考えると増幅度GVの対数をとり 　 　 として計算した方が人間の感覚に近い出力電圧が得られる。また，対数をとることにより大きな数の有効数字が少なくできて計算がしやすくなる利点もある。 　（5・3）式の対数log10は10を底とした常用対数で，係数20は電圧や電流の場合の定数である。（5・3）式のように対数をとる場合の量をデシベルと呼び，（dB）で表す。 　dBのdは英語の10，decimalから10を底とする対数，及びBは電話の発明者Bellからとった量でBは名前なので大文字を使う。 　 20log10GV=GV　（dB）　（5・4） 　 と表せる。GV（dB）からV0やViを求めるには（5・4）式から逆算して 　 　 から計算できる。（5・4）式または（5・5）式の計算は，電圧，電流，抵抗などの計算に適用される。電力のデシベル計算は定数が10となり 　 GP(dB)=10log10GP　（5・6） 　 となる。GPは電力増幅度で，入力と出力電力をそれぞれPiとP0とすると 　 　 となる。電力増幅度GP（dB）からPi，P0を逆算するには（5・5）式と同様に 　 　 となる。電力のdBでは定数が20ではなく10となることに注意が必要である。表5・4に2つの数が比のA/Bの倍率とデシベルの関係を示す。 　 表5・4 デシベル表 　 　デシベルは2つの量の比A/Bを表すので単位はないがBをある基準値とするとGデシベルからAの値を知ることができる。Bを1ボルトとしたときのある電圧Aの電圧値はGV，デシベルが既知の場合（5・3）式，（5・4）式でV0=A，Vi=B=1とおいて 　 　 となる。この場合Gは（dBV）と書いて1ボルトを基準としたデシベルであることを示す。GV=20（dBV）のときは（5・8）式から 　 20=20log10Aより　1=log10A　（5・10） A=10のとき log1010=1　（5・11） となるのでAはB=1ボルトの10倍からA=10ボルトと求められる。 　B=1μV=10-6Vを基準にしたときはG（dBμ）としてμをつける。 　電力Gのデシベル表示で，1Wを基準としたときはG（dBW），1mWを基準にしたときはG（dBm）として表示される。 デシベル表示が単なる比を表すか又は基準値による絶対値を表すか注意する必要がある。 　表5・4において倍率A/B=1に基準値Bを入れると倍率がAの値になる。 　GVが60（dBV）は倍率が1000であるので基準B=1Vに対してA=1000Vとなる。 　GPが20（dBm）のときはB=1mWの100倍となるのでA=100mWとなる。 　表5・4に示すように倍率が10倍となると電圧では+20dB，電力では+10dB増加する。逆に倍率が10分の1に下がるときは電圧で-20dB，電力で-10dBづつデシベル値が小さくなる。 　倍率が2倍のときは電圧で+6dB，電力で+3dB増加する。倍率が2分の1となると電圧で-6dB，電力で-3dB，デシベル値が小さくなる。 　dBからの逆算は電圧，電流では（5・5）式，電力では（5・8）式から計算できる。

5・3 測定値と誤差 5・3・1 誤差 　測定値にはいろいろな原因による誤差が含まれる。誤差を分類すると 　 　 　系統的誤差は予測や補正が可能だが偶然誤差は突発的た起きるので対応ができない。 　理想として求める測定値を「真の値，T」とする。「測定値，M」が得られたときの誤差εは ε=M-T　（5・12） 誤差百分率ε（％）は 　 　 と定義される。計器の等級は誤差百分率を示し，1級の計器は誤差が定格値の1%以内であることを表している。 　 5・3・2 有効数字 　測定値は数字で示される。測定値の中の誤差がある数字を沢山並べても意味がない。数字の中から必要な数字を有効数字と呼ぶ。有効数字は無効数字を四捨五入して表示する。円周率π=3.141592・・・は無限に続く数であるので計算に必要な有効数字に四捨五入する。 3桁のπ=3.14・・・4桁目の1以下は切り捨てる。 4桁のπ=3.142・・・5桁目の5は繰り上がって4桁目の1が2となる。 　測定値の有効数字に注意が必要である。3.140の測定値の意味は 5桁目が4以下で切り捨てた場合：3.1403→3.140 5桁目が5以上で繰り上げた場合：3.1395→3.140（4桁目も繰り上げられて3桁目が3から4に上がる） 3.140の4桁目の0には5桁目で四捨五入をしたことが意味されている。同様に3.1400の指示値は6桁目の測定値を四捨五入したことを示している。このように測定値の最後の桁に0がある場合に0を勝手に取り去ることはできない。測定値の計算に有効数字を考慮する必要がある。2つの測定値を加える場合 A=3.14，B=0.00053 のときA+B=3.14+0.00053=3.14053 と書いてもAの小数点以下3桁目に誤差が含まれているので小数点以下4桁目に有効数字があるBの測定値はAの誤差の中に含まれてしまうのでA+B=3.14とする。 　有効数字が指定されていない場合の測定値は通常3桁で表示する。

5・4 測定器と測定法 5・4・1 指示電気計器 　電流や電圧等の電気のエネルギーで指針などを動かして電気の量を指示するのが指示電気計器（メータ）である。 　メータを駆使する原理により種類が分類される。表5・5にメータの種類と主な用途を示す。代表的な電圧と電流の測定範囲も示した。 　メータの表面は図5・2に示す記号が書かれている。記号にはJIS規格，製造者，測定法の原理，階級（誤差）等が書いてあるので目的に応じてメータを選ぶことができる。 　 表5・5 メータの種類と用途 種類 略号 使用回路 電流〔A〕 電圧〔V〕 計器の用途 可動コイル形 M 直流 5×10-6〜102 10-2〜6×102 電圧計、電流計 抵抗計、回転計 温度計、照度計 磁束計 可動鉄片形 S 交流 10-2〜3×102 10〜103 電圧計、電流計 抵抗計、回転計 電流力計形 D 交直流 10-2〜20 1〜103 電圧計、電流計 電力計、周波計 整流形 R 交流 5×10-4〜10-1 3〜103 電圧計、電流計 抵抗計、周波計 熱電形 T 交直流 10-3〜5 0.5〜150 電圧計、電流計 電力計 静電形 E 交直流   1〜5×105 電圧計、抵抗計 誘導形 I 交流 10-1〜102 1〜103 電圧計、電流計 電力計、回転計 可動コイル比率計形 XM 直流     抵抗計、温度計 振動片形 V 交流     周波数計、回転計 可動鉄片比率計形 XS 交流     力率計、周波数計、同期検定器 電流力計比率計形 XD 交直流     周波数計、磁束計、同期検定器 電量計 　 図5・2 メータの表示 　 （a）規格記号 （e）周波数 （i）製造年月日 （b）製造者名 （f）階級 （j）その他の必要事項 （c）計器番号 （g）動作原理   （d）測定量の単位 （h）回路の種類   　 5・4・2 電子メータ 　機械的に駆動する指針に変わって発光ダイオード，液晶，CRT等を用いた電子メータが使用されている。デジタル表示やグラフィク画面表示ができるなど新しい表示器として注目されている。図5・3（a）に透過型液晶LCDを用いた電子メータの断面図を示す。後からハロゲンランプで光を投影してLCD上にメータ表示をする。（b）に電子メータのブロック図と表示を示す。 　電子メータは可動部分がないので堅牢で指針のゼロ調整が不要である。表示画面には指針型と類似，デジタル数字あるいは棒グラフ等自由な画面が表示できる。新しい指示計器として電子メータの普及が広がると考えられる。 　 図5・3 電子メータ 　 5・4・3 回路試験器（テスター）と電流分流器 　電流・電圧・抵抗等主な電気の量をまとめて測定できるのがテスターである。図5・4にテスターの外観図と測定回路を分離して示した。各回路の動作は後で説明する。交流電流は整流器で直流に交換して直流電流として測定する。メータは可動コイル型直流電流計でアナログ表示をするかデジタル電圧としてデジタル表示をする。図5・4はアナログ型のテスターを示す。電気の種類と測定範囲（レンジ）はスイッチで切り替える。 　 図5・4 テスターと回路図 　 　図5・5に可動コイル型直流電流計の構造を示す。永久磁石NとS極の間に回転できる可動コイルを入れ，コイルに電流を流すと磁界と電流との相互作用（フレミングの左手の法則と呼ぶ）によりコイルが回転する。コイルに取り付けた指針も回転する。回転角度が電流の大きさに比例することから電流値が表示できる。可動コイル型電流計は精度がよく安定した直流電流が測定できるので標準計器とされている。 　 図5・5　可動コイル型電流計 　 図5・6 電流の分流器 　 　図5・6は電流計の測定レンジを拡大する分流器回路を示す。定格値（フルスケール）がig，（A），内部抵抗g（Ω）の電流計の定格値をm倍に拡大する場合に（a）普通分流器では電流計に並列に分流抵抗Sを挿入するとき外部から流し込める電流Iとigの間には 　 　 Iを定格値igのm倍とするため 　 mig=I　（5・15） 　 として（5・14）式を書きなおすと 　 　 となるので電流計内部抵抗gの（m-1）分の1の分流抵抗Sを電流計に並列に加えると測定レンジがm倍となる。 　 　 となるのでSを切り替えると測定レンジを替えられる。しかし，Sを切り替えるとメータの応答性が変化して指針の動き速度が変化する欠点がある。これを解決したのが（b）の万能分流器である。Sの値は変えないで，Sの途中から電流端子を接続する。端子の位置をSの左からS/n，右から（S-S/n）の位置とすると 　 I=(nm)ig　（5・19） 　 となり，m倍から更にnm倍にレンジが拡大される。Sを一定として端子の位置nを切り替えることから指針の速度が変わらないでレンジ切り替えができる。

5・4・4 交流計器の波形誤差 　可動コイル型電流計と整流器を組み合わせると交流の電流及び電圧が測定できるがコイルを駆動する力は交流の平均値である。通常，交流は実効値で取り扱われる。家庭用の100V電圧は実効値100Vの交流である。このためメータの目盛りを実効値に変換してある。最大値VPの交流の実効値と平均値との比を波形率と呼ぶ。 　 　 より可動コイル電流計で交流を測定したとき指針の駆動力は平均値なので実効値に換算した 　 目盛り＝指針の駆動力（平均値）×1.11（波形率）＝実効値指示　（5・21） 　 となるように交流の波形率1.11倍の目盛りで読み取ることにしてある。しかし，パルス波のように正弦波でない波形では波形率が1.11倍とならないので読取りに波形誤差が生ずる。 　一般に正弦波でない波形を整流計器で測定すると波形誤差を生ずるので実効値を指示する熱電対型電流（電圧）計のように波形に影響されない計器を使用する必要がある。 　 5・4・5 電圧計と倍率器 　アナログ型テスターの電圧計は，電流計に直列に外部抵抗を接続すると電圧計となる。外部抵抗の値を切り替えることから電圧計のレンジ切り替えができる。このときの外部抵抗を倍率器と呼ぶ。 　図5・7（a）に電流計Mに倍率器Rを直列接続した電圧計を示す。（b）は電圧計のレンジ切り替え回路を示す。 　 図5・7 倍率器付電圧計 　 　（a）において電流計Mは内部抵抗rをもつので電流計の端子電圧EVは定格電流をIとすると EV=I×r　（5・22） となるが，この値は小さくて数mV〜数十mV程度なので大きな電圧を測定するには倍率器Rが必要になる。電流計の端子電圧EVのm倍の測定端子電圧Eとするための倍率器Rの値を計算する。電流計定格電流Iから E=IR+Ir=I(R+r)　（5・23） E=mEV=mIr　（5・24） の2つの式からEとIを消去すると R=(m-1)r　（5・25） となるので，電流計の内部抵抗rの（m-1）倍の倍率器を直列に接続すればレンジがm倍となる。倍率mは（5・24）式から 　 　 となるので（b）図のように倍率器Rを切り替えて電圧計のレンジが拡大できる。 　 5・4・6 デジタルボルトメータ 　アナログ電圧をアナログ／デジタル変換器（ADコンバーターとも呼ぶ）によりデジタルパルスに変換して計数回路によりパルスの数からアナログ電圧を測定するデジタルボルトメータの系統図を図5・8に示す。 　 図5・8 デジタルボルトメーターの系統図 　 　雑音混入による誤動作を防ぐため二重積分型ADコンバータによるボルトメータが普及している。図5・9にその回路構成と原理図を（a）と（b）に示す。測定電圧VXと比較する基準電圧VSをそれぞれ積分器で積分してアナログ電圧に比例した計数パルス，をつくりそれぞれの計数値N1とN2及び安定した基準電圧VSのみから測定電圧VXが求められる。 　 図5・9 二重積分型ADコンバータによるデジタルボルトメータ 　 　始め入力スイッチS1はA端子，積分器スイッチはS2をONからOFFとすると測定電圧VXが積分されて積分器出力は（b）のように時間t1から直線的に降下する。ゼロ検出用コンパレータ出力がV0に到達する時間t2までクロックパルスが制御回路を通ってカウンタに送り込まれパルス数N1が求められる。t2の時間からS1はB端子へ切り替えられてマイナス極性の標準電圧，-VSにより積分器出力は（b）に示すようにt2から直線的に上昇する。時間t3で初期電圧0に戻る。t2〜t3の間のクロックパルス数N2をカウンタで計数する。 　測定電圧VX，出力電圧V0，と時間t1〜t2の間の関係は 　 　 ここで，CRは積分器の時定数である。時間t2〜t3ではV0から0まで上昇するので 　 　 両式から測定電圧VXを求めると 　 　 となり，パルス数と標準電圧だけから測定電圧VXが求まる。積分器により回路の変動や雑音の妨害が除去されて安定なデジタル電圧計となる。積分器のS2はONにすると積分器出力を0の初期条件に戻す役目をする。 　 5・4・7　抵抗測定（オームメータ） 　抵抗測定には，電圧・電流計法，ブリッジ法，オームメータ法，絶縁抵抗計（メガー）等がある。ここでは図5・4のテスターに使用されているオームメータを説明する。図5・10（a）にオームメータの原理図，（b）にオームメータの目盛りを示す。 　 図5・10 オームメータ 　 　電流計A，電池E，電流計内部抵抗も含めた直列抵抗rの回路に測定する抵抗Rを接続する。回路に流れる電流はオームの法則から 　 　 　測定端子をショートしたときの回路電流I0は（5・30）式でRを0とすることから 　 　 （5・30）式と（5・31）式からEを消去すると 　 　 （5・32）式は電流比（I/I0）と抵抗比（R/r）の関係が双曲線となることを示す。ショート電流I0がメータのフルスケールとなるように始めに調整しておけばメータの指示値Iで測定する抵抗値Rを直読することができる。（b）図にオームメータの目盛りを示す。R=0のショート電流I0でフルスケール，開放R=∞で0の目盛りとなる。

5・4・8 電力測定 　電力の測定法には，電流・電圧計法，抵抗・電流計法，電流力計形法，サーミスタ／バレッタ法，カロリーメータ法等がある。ここでは電圧・電流計法と抵抗・電流計法について説明する。図5・11に負荷抵抗Rで消費する電力測定回路を示す。 　 図5・11 電圧・電流計による電力測定 　 　（a）は負荷と並列に電圧計Vがある場合，（b）は負荷と直列に入れた電流計Aに電圧計を接続した場合である。電圧計の内部抵抗RVと電流計の内部抵抗RAが無視できないとき（a）と（b）では誤差が異なる。負荷抵抗Rで消費される電力Pは （a）の接続では，P=EI-E2/RV　（5・33） （b）の接続では，P=EI-RAI2　（5・34） となる。EとIは電圧計と電流計のそれぞれの指示値である。電圧計の内部抵抗RVが大きく，電流計の内部抵抗RAが小さい場合は（a），（b）ともに内部抵抗を無視できて P≒EI　（5・35） と近似できるので，電圧計と電流計の指示値の積が電力を示す。 　負荷抵抗Rが既知の場合にはオームの法則から 　 を（5・35）式に代入して 　 　 又は 　 　 から電流計又は電圧計と負荷抵抗Rの組合せで電力が測定できる。 　 5・4・9 波形測定 （A）アナログオシログラフ 　ブラウンが発明した陰極線管（ブラウン管）の蛍光面に測定信号波形を表示して，波形，周期，周波数等を観測する測定器で，パルス波やビデオ等正弦波でない信号の測定に適している。図5・12にオシログラフの構造を示す。 　 図5・12 オシログラフ 　 　ブラウン管はテレビにも使用されている。電子銃から飛び出した電子ビームが水平と垂直偏向板の間を通過するとき電子ビームの軌道が曲げられ，更に進行して蛍光面に衝突して発光する。水平偏向板にのこぎり波を加えると電子ビームが水平方向（時間軸という。）に等速度で移動する。測定する電圧を垂直偏向板に加えると電圧に比例して電子ビームが垂直（上下方向）に動くので波形の観測ができる。（b）図のようにブラウン管蛍光面が表面となる。 　テレビは水平と垂直偏向板にのこぎり波を加え，ビデオ信号で電子ビームを変調して蛍光面上の輝度を変化させてテレビ画面を表示する。 　 図5・13 オシログラフの回路系統図 　 　図5・13に回路系統を示す。水平軸へ加えるのこぎり波の周期と垂直軸に加える信号波の周期が整数比のときだけ波形が静止して表示される。このため垂直軸から信号波を取出して時間軸発振器に入力し，周期信号を発生させ水平軸のこぎり波の周期を制御して信号波形を静止させる。また，外部から任意の信号を時間軸発振器に加えて外部信号で同期をとることもできる。同期をとることをトリガと呼ぶ。 　水平軸端子から外部信号を水平軸用増幅器を通して水平偏向板に加えることから周波数測定等波形観測以外の応用が可能となる。 （B）デジタルオシログラフ 　一般にはオシログラフといえばアナログ信号波形を表示する機器をいう。デジタルオシログラフはアナログ信号をデジタル変換して，メモリや演算処理をしてから再びアナログ信号に戻してブラウン管上に表示する測定器で，従来のオシログラフでは不可能な新しい機能を持っている。コンピュータと組合わせたオシログラフである。表5・6にアナログ式とデジタル式オシログラフの機能の相違を比較して示した。 　 表5・6 アナログとデジタルオシログラフ比較表 機能 方式の違い  アナログ方式 デジタル方式 単発現象 観測 基本的に不可（蓄積管を使えば可能） 可能 プリトリガ 数10〔ns〕が限度 長時間可能 演算 ＋， −などの単純な演算のみ 高度の演算処理が可能 自動判定 不可 可能 波形保存 不可 長時間可能 データ出力 不可 可能　プリンタ， GP-IB， 　RS-232Cなど 　 デジタルオシログラフの優れた機能は 1. 単発現象の観測が可能；1回しか表れない波形をアナログ式で観測するには波形の立ち上がり時間と同期して水平軸のこぎり波をスタートさせることができない。デジタル式では信号をメモリーできるので任意の時間からの波形を取り出して表示できるので電源起動時の波形や単発ノイズ等を取り出して観測できる。 2. プリトリガ；アナログ式では信号のあるレベルを同期トリガとするのでそれ以後の波形しか観測できない。デジタル式では同期トリガ以前の波形がメモリされているので呼び出して表示できる。 3. 演算処理；デジタル式にはコンピュータが組み込まれているので入力信号を演算処理してから表示できる。処理には，平均値演算，フーリェ変換，相関関数等があり，リアルタイムで演算された波形が表示できる。 　その他表5・6に示した特色を持っている。図5・14にデジタルオシログラフの構成と外観を示す。 　 図5・14 デジタルオシログラフの構成と外観

5・5 信号と高周波の測定 5・5・1 周波数の測定 　代表的なアナログ周波数測定はオシログラフによるリサージュ図形法で，デジタル周波数測定は周波数カウンタである。 （A）リサージュ図形法 　図5・15のようにオシログラフの垂直軸（Y軸）に被測定発信器，水平軸（X軸）に標準発振器を接続すると画面にリサージュ図形が表れる。標準発振器の周波数を変化するとX軸とY軸の周波数が互いに整数比のときリサージュ図形が静止する。このときの図形から被測定発振器の周波数が求められる。（a）に測定法の構成，（b）にXとYに同じ周波数と振幅を持ち，位相差が90度の正弦波を加えたとき表れる円形のリサージュ図形を示す。（c）はX: Yの周波数比がそれぞれ，1: 1，1: 2及び1: 3のときのリサージュ図形を示す。同じ周波数比でも位相差が変わるとリサージュ図形が変化するので読取りに注意が必要である。標準発振器の周波数を基準としてリサージュ図形から被測定周波数が精度よく測定できるので低周波帯での周波数測定が行われている。 　 図5・15 リサージュ図形法周波数測定 　 （B）周波数カウンタ 　周波数とは1秒間における電気の波の振動数である。50HZは1秒間の50回振動する交流である。被測定信号を1秒間取り出して（ゲートとよぶ）電気振動の数を直接計数する測定器が周波数カウンタである。ゲートする時間は1秒間でなくてもよく0.1秒間なら計数値を10倍，0.01なら100倍とすれば周波数が求められる。 　図5・16に周波数カウンタの外観図（a）と加える波形を示す。正弦波入力（b）をパルスに変換して入力パルス列Aとして（c）のゲート回路に加える。ゲート電圧Bが加えられた時間だけゲート回路が開き，入カパルス列がゲートを通過して計数回路で計数されデジタル数字で表示される。（d）に各部における波形関係を示す。ゲート時間幅が広いほど有効数字が多く読み取れる。 　ゲート幅を1/n秒間としたときのカウンタの計数値をNとすると，被測定信号の周波数fは f=nN　（HZ）　（5・39） 数ヘルツ以下の低い周波数では被測定波形からゲート信号Bをつくり，パルス発生器から取り出した計数パルス列Aを計数する。被測定波形の1周期Tを計数するのでこの方法を周期カウンタ法と呼ぶ。計数値をNとすると被測定周波数fはf=1/T，計数パルスの周波数をfS，周期をtS=1/fSとすれば 　 　 として求められる。 　 図5・16 周波数カウンタ

5・5・2 周波数スペクトル 　信号を周波数単位のエネルギー分布で表すと周波数スペクトルとなる。図5・17（a）にある信号の3次元表示を示す。基本波と2倍高調波の正弦波が合成されている。時間軸でこの波形をオシログラフで観測すると（b）の点線で示すそれぞれの正弦波が合成されて実線のような正弦波でない波形に観測される。 　この信号をスペクトルアナライザにより周波数軸上で観測すると（c）に示すように2本のスペクトルとして分離して表示できる。 　 図5・17 信号の3次元表示 　 （A）アナログスペクトルアナライザ 　図5・18にスペクトルアナライザの原理図と外観図を示す。被測定信号にいくつかの周波数成分が含まれているとする。その内のfS成分を抜き出して表示するにはローカル発振器から信号f0を発生してその間の差周波数fiを周波数変換器とバンドパスフイルタを通してオシログラフの垂直軸（Y軸）に加える。 　Y軸の振幅は差周波数fi fi=fS-f0　（5・42） のエネルギーを表示する。バンドパスフイルタは狭帯域で一定のfi成分のみを通過させる。ここでローカル発振器の周波数f0を直線的に変化するとf0よりfiだけ高い信号のfS成分のエネルギーのみがY軸に入力される。一方，ローカル発振器の周波数を直線的に変化させるためののこぎり波をオシログラフの水平軸（X軸）に加えるとローカル発振器の周波数に比例したX軸が掃引されるので周波数スペクトルが表示できる。 　 図5・18 アナログスペクトルアナライザ 　 （B）デジタルスペクトルアナライザ 　時間波形から周波数スペクトルに変換するには数学的なフーリェ変換を計算することによる。図5・19のようにオシロスコープに表示されるのは信号の時間波形で，フーリェ変換することによりスペクトルに変換される。 　 図5・19 時間波形から周波数スペクトルヘの変換 　 　デジタルスペクトルアナライザはアナログ信号をデジタル信号に変換してから高速フーリェ変換（FFTと呼ぶ）演算をコンピュータで行いデジタル周波数スペクトルとしてオシログラフ上に表示する測定器である。図5・20に構成を示す。 　 図5・20 デジタルスペクトルアナライザの構成 　 FFT演算によるデジタルスペクトルCKは 　 　 信号XjはデジタルスペクトルCKを逆FFT演算して 　 　 から求められる。ここで，Nはデジタル標本化数，CKは標本化したk番目のスペクトル成分，Xjは波形を標本化したときのj番目の振幅成分を表す。 　デジタルスペクトルアナライザは信号をデジタル化してXjを（5・43）式によりN回の計算を行うとk番目のスペクトルCKが求められるので，さらにkについて0〜N-1， のN回計算をして全スペクトルが求められるので，N×N=N2回の計算が必要となる。詳細なスペクトルを求めるため標本化数Nを大きくとると膨大な計算が必要となる。 　CoolyとTukyは高速フーリェ変換（FFT）と呼ぶソフトウエアを発見して計算する回数を大幅に少なくすることに成功した。 　FFTでは標本化数Nを二つの整数PとQの積に分解して N=P・Q　（5・45） とおいて全計算回数N2を N2→N（P+Q）　（5・46） に減少させた。例えばP=4， N=210=1024とすると計算回数は約50分の1に少なくできるので高速でスペクトル計算が可能となる。 　デジタルスペクトルアナライザはFFT計算によりほぼリアルタイムでスペクトル表示ができるようになった。

5・5・3 信号と変調 　第2章で説明したように信号にはアナログ信号とデジタル信号がありそれぞれ波形，周波数スペクトル，電力，変調度等の測定が行われる。取り扱う周波数帯により直流，低周波及び高周波帯の測定となる。低周波用の測定器は高周波帯で使用できない。正弦波の電圧計や電力計はパルス波のような非正弦波に使用すると波形誤差を生じる。特に雑音のように波形と時間がランダム（不規則）に変動する電圧を測定するときは測定器や測定法に注意が必要となる。 （A）オシログラフによる振幅変調AM波の変調度測定 　第2章2・2・3項で説明したようにオシログラフにより直接波形を観測して変調度mを求めることができる。図5・21にオシログラフに表示されたAM波形から変調度mは 　 図5・21 AM波形 　 　 から計算できる。 （B）スペクトルアナライザによるAM波の変調度測定 　スペクトルアナライザを用いるとAM波のスペクトルが観測できる。図5・22に両側波帯振幅変調波DSBAM波のスペクトルを示す。 　 図5・22 DSBAM波のスペクトル 　 　搬送波スペクトルの振幅ECと上又は下の側波帯スペクトルmEC／2の比をとると 　 　 より変調度mは 　 　 としてスペクトルアナライザにより求められる。

5・5・4 送信機の測定 　代表的な送信機の構成は第2章2・2・4項で説明してある。送信機の特性は送信周波数・送信電力，変調特性，スプリアス（送信波に寄生して発生する妨害波），安定度等で規定される。 （A）送信電力の測定 　図5・23（a）に擬似抵抗負荷法（b）に電球負荷法による送信電力測定法をそれぞれ示す。 　 図5・23 擬似負荷による送信機電力測定 　 （a）擬似抵抗負荷法はアンテナと同じ電気定数，抵抗Rと容量Cを持つ擬似負荷回路に送信機出力を加えて回路電流Iを測定すると送信電力Pは P=I2R　（5・50） から，求められる。 （b）電球負荷法は擬似抵抗負荷の代わりに負荷ランプを用いる方法で，送信電力で負荷ランプRを発光させる。これと同じ規格のランプLを直流又は交流でRと同じ輝度になるまで発光させるときランプLに消費される電力から送信機から負荷ランプに加わる電力Pを求める方法である。負荷ランプの抵抗をアンテナ抵抗と等しくする必要があるが直流又は交流用の電圧計と電流計で高周波電力の測定ができる利点がある。 （B）送信周波数の測定 周波数の測定は 1. 周波数の確度； 　規定した送信周波からのずれの値を確度という。一般に時間と共にずれの値が変化する。この変動の大きさを周波数安定度という。周波数の測定は周波数カウンタで測定できる。周波数安定度は安定な信号発生器の出力周波数と送信機周波数との間をオシログラフによりリサージュ図形を描かせることから測定できる。 図5・24に周波数カウンタによる送信機の周波数測定の構図を示す。 　 図5・24 送信機の周波数測定 　 　送信機と周波数カウンタとの結合は送信機に影響を与えないようにできるだけ疎結合とする。周波数カウンタ入力端子に短いアンテナを立てて結合させることができる。 　リサージュ図形による周波数測定は5・5・1（B）項に説明してある。高周波の周波数が高いとき直接オシログラフで観測できないときは周波数変換器で周波数を低く変換して観測するが変換用の局部発振器の変動が誤差に加わる。 2. 周波数スペクトル； 　送信機から放射される電波の周波数スペクトル及びスプリアス（不要放射）はスペクトルアナライザで測定される。 　図5・25にスペクトル測定の構成図を示す。 　 図5・25 送信機出力のスペクトル測定 　 　一般に高い周波数はアナログスペクトルアナライザ，低い周波数スペクトルはデジタルスペクトルアナライザが使用される。周波数を変換することからミリ波や光の波長のスペクトルまで測定できる測定器が市販されている。スペクトルアナライザは送信機から放射される不要電波（スプリアス）の測定にも使用される。

5・5・5 受信機の測定 　図5・26にスーパーヘテロダイン受信機の構成図を示す。 　 図5・26 スーパーヘテロダイン受信機 　 　受信機の性能は，感度，選択度，忠実度，雑音指数NF，等で表せる。図5・27に受信機の総合特性を測定する測定器の構成図を示す。 　 図5・27 受信機総合特性測定構成図 　 　信号発生器出力を擬似空中線回路を通して受信機に入力する。擬似空中線回路はアンテナと同じインピーダンス（高周波抵抗）を持つ回路で，アンテナを接続したときと同じ状態とするためである。出力スイッチSを1にするときは音声出力がマイクロホンで検出されて音質（忠実度）が測定される。 　スイッチSを2にするときは負荷抵抗から電気的な低周波出力を取り出して出力計により受信機出力を測定する。また，ひずみ率計により電気的に忠実度を測定する。 （A）感度の測定； 　図5・27で出力スイッチSを2の位置で感度を測定する。出力計で標準出力（放送用は50mW，商用は10mW）となるときの受信機に加える信号発生器出力を，受信周波数を変えて測定すると図5・28（a）に示すような感度特性が得られる。 　 図5・28 受信機の感度と選択度特性 　 　標準出力となるときに入力に加える電圧が小さいほど感度がよい受信機となる。 （B）選択度の測定； 　選択度は受信する周波数以外の周波数を抑圧する能力で，混信を防ぐ特性をいう。選択度の測定は図5・27の構成で出力スイッチSを2の位置とする。選択度の測定法には入力電圧を一定として受信機を同調周波数に固定したまま，信号発生器周波数を変化したときの出力計の読みから求める入力一定法と，出力電圧を一定に保つように信号発生器周波数を変化しながら信号発生器電圧を変化させたときの受信機入力電圧から選択度を求める出力一定法がある。受信機が飽和することなどから一般には出力一定法が行われている。 　図5・28（b）に出力一定法による選択度特性の一例を示す。横軸は信号発生器の周波数と受信機の同調周波数の差（離調周波数），縦軸は出力一定となるために必要な信号発生器出力電圧を同調周波数における入力電圧を基準とした相対入力電圧で示した。選択度がよい受信機ほど幅が狭い曲線となる。（b）は同じ受信機でも同調周波数が1000KHzより600KHzのときの方が選択度が良くなっている特性を示している。 （c）忠実度の測定； 　忠実度は変調信号の周波数特性を示す。音響機器等では低音から高音まで広い周波数の音声が再生できることが要求される。受信機の周波数帯域幅に関係する特性で，デジタル機器では受信機の帯域幅が狭いとパルス波形が崩れて正確にデジタル信号が取り出せなくなる。忠実度の測定は図5・27の構成で出力スイッチSを1にすると音響忠実度が求められる。Sを2とすると電気的忠実度が求められる。測定法は受信機の同調周波数に信号発生器出力周波数を一致させる。受信機入力電圧も一定としたまま低周波発振器周波数を変化させると図5・29に示すような忠実度特性が得られる。横軸は変調周波数（低周波発振器周波数）縦軸は出力計の読みを1000Hzを基準として相対出力（dB）で表してある。変調周波数が低いときと高いときは1000Hzのときより忠実度が悪くなることが示されている。図には音響的と電気的忠実度が比較して示してある。 　 図5・29 忠実度特性の一例

5・5・6 アンテナの測定 　アンテナの特性は，実効抵抗，指向特性，利得，利得対雑音比G/T等で表せる。 （A）アンテナ実効抵抗の測定； 　図5・30にアンテナ実効抵抗の測定回路構成図を示す。送信機出力をスイッチ回路を通してアンテナに接続する。アンテナ同調周波数と送信周波数が一致するとアンテナに流れる電流Aが最大となる。次にスイッチを擬似空中線回路に切り替える。コイルまたはコンデンサの大きさを可変して電流計Aの指示値を最大にする。さらに可変抵抗Rを変化して電流計Aの指示値がアンテナを接続したときと同じ値にすると，このときの可変抵抗の値がアンテナ放射抵抗となる。また，可変コイルのインダクタンスL又は可変コンデンサの容量CがアンテナのインダクタンスL又は容量Cと等しくなっている。 　 図5・30 アンテナ放射抵抗の測定 　 （B）アンテナ利得の測定； 　アンテナ放射電力を目的方向に能率よく放射するためアンテナに指向性を持たせる。ある指向性アンテナに一定の電力を供給して電波をある距離に固定した受信アンテナで受信する場合を考える。そのときの受信電力をPTとする。次に指向性アンテナの位置に無指向アンテナを置き同じ電力で電波を放射する。始めと同じ受信機でこの電力を受信した電力をP0としたとき指向性アンテナの利得GAは受信電力比 　 　 となる。GAは無指向性アンテナに対する利得なので絶対利得という。基準アンテナをダイポールアンテナとしたときの指向性アンテナの利得を相対利得GRと呼ぶ。絶対利得GAと相対利得GRとの関係はダイアポールアンテナの絶対利得をGdとすると 絶対利得GA＝相対利得GR×ダイポールアンテナの絶対利得Gd　（5・52） となる。ダイポールアンテナの絶対利得Gdは約1.64なので（5・52）式は GA=GR×1.64　（5・53） となる。dBに換算して表すと GA(dB)=GR(dB)+2.15(dB)　（5・54） となる。あるアンテナの利得測定は図5・31に示すように利得が判っている標準アンテナとの比較により求められる。送信アンテナから離れた距離に測定する試験アンテナと標準アンテナを設置して受信する。同一の場所に置くことが望ましい。 　 図5・31 アンテナ利得測定法構成図 　 　送信アンテナから一定の電力を送信する。まず標準アンテナで受信したときの電力をPRとする。次に試験アンテナに切り替えて受信する。この時の受信電力PTが PT=PR　（5・55） となるように可変減衰器を調節する。試験アンテナ利得GA，標準アンテナ利得GR，可変減衰器の減衰量（出力／入力）Lとすると 　 　 減衰量1/L，利得GをdBで表示すると試験アンテナ利得GA（dB）は GA(dB)=GR(dB)+L(dB)　（5・57） で求められる。 （C）指向性（アンテナパターン）の測定； 　アンテナ指向性は測定するアンテナを回転台の上に乗せて離れた場所から放射された電波を台を回転しながら受信する方法で測定される。図5・32（a）に指向性測定構成図を示す。送信と受信アンテナ間の距離は遠方電界となるだけ離すことが必要であるが，距離が大きく取れないときは測定値を計算で補正する方法が行われている。周囲からの妨害電波が入ってこない場所が必要で電波暗室内で測定する場合が多い。回転台やケーブル等からの反射波が混入しないように電波吸収材で覆うなどの対策が必要となる。送信と受信アンテナの偏波面を一致させること，アンテナの高さを調節して主ビームの中心で受信することなどの注意が必要となる。測定アンテナの位置での電界の強さを求めるための参照信号受信用アンテナを付加する場合がある。（b）に測定された指向性の一例を示す。周囲からの妨害波が混入するので室外でレベルの低いサイドローブを正確に表示することは困難である。 　 図5・32 アンテナ指向性の測定

5・5・7 電界強度の測定 　ある場所における電波の強さは電界強度又は磁界強度で表せる。電界強度は1m離れた2点間の電波の強さの差で表せるので単位が（V/m）となる。 （A）アンテナ係数法 　電界強度E（V/m）の空間にアンテナ係数AFのアンテナを置くときアンテナに誘起する電圧Vとの間には 　 　 の関係がある。アンテナ係数AFが知られているアンテナで電波を受信したときのアンテナ出力電圧Vが測定できればその場所の電界強度Eは（5・58）式から E=AF・V　（5・59） として求められる。図5・33にアンテナ係数による電界強度測定系を示す。電波が大地や壁などから反射して直接波に混入すると誤差を生ずる。 　電磁両立性EMCにおいてある機器から放射される不要電波の強さの測定は大地反射波の影響を考慮したアンテナ係数を用いて放射電界の強さを測定する。 　 図5・33 アンテナ係数による電界強度測定系 　 （B）電界強度測定器 　電界強度測定器は標準アンテナ，比較信号発生器，受信機と出力計を組み合せた構成により長波，中波及び短波帯の電界強度を測定する機器である。図5・34に電界強度測定器の構成図を示す。 　 図5・34 電界強度測定器 　 　電界強度E（dB）の電波を実効高Hのアンテナで受信するようにスイッチを（1）にする。受信機の利得G（dB）を調節して出力P（dB）が規定値となるようにする。スイッチを（2）に切り替えて比較信号発生器から電界と同じ周波数を発生する。その出力E0（dB）を減衰器を通して受信機に加えて出力計の読みが同じP（dB）となるように減衰度α（dB）を調整すると電界強度E（dB）は E+H+G=E0-α+G=P　（5・60） より E=E0-α-H(dBμ)　（5・61） として測定できる。電界強度（dB）は1μVを基準とした（dBμ）で表示される。ループアンテナの実効高H（dB）は 　 　 である。ここでAはループアンテナの面積，Nはループアンテナの巻数，πは円周率，λは波長を表す。

5・5・8 電磁両立性EMCの測定 　一般的なEMCの定義，規格及び測定法については第4章4・8項で説明してある。 　ここでは船舶に関係するEMC規格「IEC60945］に関連した測定法について補足説明をする。IEC60945は「航海及び無線連絡装置と設備−試験方法及び所要試験結果」を取り扱う国際EMC規格である。 EMCの測定は （A）機器から放射される「好ましくない電磁放射（妨害波）」に関する測定，と（B）妨害波に対して「電磁妨害の存在する環境で，機器，装置又はシステムが性能低下せずに動作することができる能力（イミュニティ）」に関する測定，に分けられる。 （A）妨害波放射に関する測定 　図5・35に試験機器から放射される電磁放射レベルの測定系を示す。回転台上に供試機器を乗せて回転しながら3〜10m離れた受信アンテナにより妨害波電界強度を測定する。アンテナのアンテナ系数AFは予め較正しておく。アンテナの高さを1〜4m，又は2〜6m上下させて妨害波レベルを測定する。放送電波など他からの混信を避けるため電波暗室内又は電波環境が良い野外のオープンサイトで測定する。 　 図5・35 妨害波レベルの測定系 　 図5・36 妨害波の許容レベル 　 　機器から3m離れた位置におけるIEC60945で規定される妨害波の許容値を図5・36に示す。図の横軸や測定周波数，縦軸は許容値を示す。下にあるほど厳しい許容値となる。150MHz帯は海上での通信機周波数があるため24（dBμ）と最も厳しい規制値とされている。 　妨害波は電波として放射される以外に電源や信号ケーブル等を経由して供試機器に影響を与える伝導による放射妨害がある。表5・6に伝導による放射妨害と電波幅射による放射妨害の測定条件を示す。 　 表5・6 妨害波測定の試験条件   携帯式 防護式 露出式 浸水式 伝導による放射   10kHz−150kHz　　　63mV−0.3mV 　　　　　　　　　　　　　（96dBμV−50dBμV） 150kHz−350kHz　　　1mV−0.3mV 　　　　　　　　　　　　　（60dBμV−50dBμV） 350kHz−30kHz　　　0.3mV（50dBμV） 幅射による放射 150kHz−300kHz　　　10mV/m−316μV/m 　　　　　　　　　　　　　　（80dBμV/m−52dBμV/m） 300kHz−30MHz　　　316μV/m−50MV/m 　　　　　　　　　　　　　　（52dBμV/m−34dBμV/m） 30MHz−1GHz　　　　　500μV/m except for 　　　　　　　　　　　　　　（54dBμV/m） ／m（24dBμV/m）   　 （B）イミュニティ測定 　ある機器が妨害波を排除する能力がイミュニティである。表5・7にイミュニティ測定の項目を示す。 　 表5・7 イミュニティ測定項目   携帯式 防護式 露出式 浸水式 伝導低周波妨害 * 10%　交流供給電圧　50Hz〜900Hz 10%〜1%　900Hz〜6kHz， 1%　6kHz〜10kHz 10%　直流供給電圧　50Hz〜10kHz 交流と直流電源ポート， 性能基準A   伝導無線周波妨害 * 3Vr.m.s.， e.m.f.10kHz〜80MHz， 10Vr.m.s.， e.m.f指定のスポット周波数において交流と直流の電源ポート， 信号と制御ポート， 共通方式　　　　　　　　　　　　　　　　　性能基準A   放射妨害 10V/m 80MHz〜1GHz 囲い型ポート 性能基準A   * 急速過渡 （バースト） * 交流電源ポートの2kV差動 信号と制御ポートの1kV共通方式 性能基準B   迅速過渡 （サージ） * 1kV Line/earth， 0.5kB Line/Line 交流電源ポート 性能基準B   電源短期変動 * ±20% voltage for 1.5s， ±10% frequency for 5 s 交流電源ポート 性能基準B   電源故障 * 60秒遮断 交流と直流の電源ポート 性能基準C   電磁放電 6kV接点 8kV空中 性能基準B      * *該当なし 　 　図5・37に放射電磁界イミュニティ測定系の一例を示す。供試機器の周囲の電界強度が一様となることが要求される。床からの反射を消すために電波吸収材を敷く。 　 図5・37 放射電磁界イミュニティ測定系 　 　機器に照射する電界強度は表5・8のようにレベルが規定されている。 　 表5・8 イミュニティ試験照射電界強度レベル レベル 試験電界強度 V/m 1 2 3 X 1 3 10 特別 注　“X”はオープン試験レベル，本レベルは製造者仕様に示すこと。 　 　イミュニティ試験結果の評価はIEC60945により次のA，B及びCの基準で性能評価が行われる。 　 −性能基準A: EUTは試験中とその後において，その目的とするとおり動作を継続しなければならない。該当する装置の規格及び製造者が発行した技術仕様書に定められるとおり，性能劣化も機能の喪失も許されない。 −性能基準B: EUTは試験後において，その目的とするとおり動作を継続しなければならない。該当する装置の規格及び製造者が発行した技術仕様書に定められるとおり，性能劣化も機能の喪失も許されない。試験中においては，自力で回復できるか，または，制御装置の操作によって試験の最終時点に回復できる場合に限って許される。 −性能基準C: 試練中においては，機能又は性能の一時的な劣化又は喪失は，該当する装置の規格及び製造者が発行した技術仕様書の中に定められるとおり，機能が自力で回復できるか，または，制御装置の操作によって試験の最終時点に回復できる場合に限って許される。

第5章 練習問題

まず、アンテナのエレメント上では、電流分布というものがあります。輻射（受信）効率のよい部分・悪い部分をあらわしてると思ってよいでしょう。
1/2λ（半波長）ダイポールアンテナでしたら中央部分、1/4λ垂直型アンテナなら根元部分、つまり給電点近くに電流分布の大きい部分があります。

これを、エレメント全体で均等なものと考えた時の、等価的長さのことを実効長と呼んでいます。

この長さは簡単な割り算で求められます。
1/2波長ダイポールアンテナ（八木アンテナの輻射器部分にも使いますね）では、λ/π[m]　（ただしλ＝波長、300/周波数[MHz]、π＝円周率）
1/4波長垂直接地アンテナ（自動車などに取り付けるホイップ型アンテナもこれと同様に考えます）ではλ/２π[m]となります。

アンテナに誘起される電界強度は、ご質問に有りますように、電界強度Ｅ[V/m]、実効長Le[m]とすると、起電力e[V]は、e＝ＥLe[V]となります。

ご覧になった書籍は無線工学の専門書か何かでしょうか。
こういった内容でしたら、高価で入手困難な専門書よりも、上級（１・２級）アマチュア無線技士受験者用の教科書や問題集に非常にわかりやすく解説されています。
アンテナの利得を測定する場合、比較するアンテナが必要です、これを標準アンテナと言います。
標準アンテナとは、測定する周波数において、その利得が計算により求められるアンテナで、1/2λ（ラムダと呼ぶ）ダイポールアンテナが良く使用されます。
実効長１ｍのアンテナなら１５０ＭＨｚ近辺の周波数でしょうか、
計算式は　λ（メートル）=300/周波数（ＭＨｚ）
この標準アンテナと測定するアンテナを比較して、アンテナ利得を測定します。